Return to Basic Equipment Menu
|
Compasses
A compass is a tool used to make a circle, and in making
circles it can be utilized in many ways. Compasses are also
used to transfer measurements, find a center points, and
create right angles. Sometimes variations on the compass
theme can be utilized as well to create accurate ellipses,
arcs and spirals. Often underestimated, a compass is often
an extremely useful tool.
|

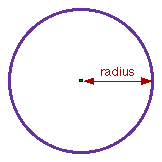
Geometrically, a circle is defined as the set of all points equal
in distance from a single central point. All compasses create circles
by first describing a radius, that equal distance between the circle
and its center. The radius can be used to designate like measurements
when necessary. The following examples are meant to show how to do a
few simple constructions with a compass. No proofs are offered
here.
Bisect a Line Segment
To bisect means to split in two equal parts. In this case, using a
compass will allow one to not only define a center point, but to
create true right angles. Variations on this theme can be used quite
efficiently for many geometric tasks.
|
|
First, make a straight line with which to work. It can
either be a random line, or one that is carefully
placed.
|
|
|
Place a couple of dots on the line to define endpoints of
a segment. These dots can be carefully measured if
necessary, or arbitrary if it does not really matter.
|
|
|
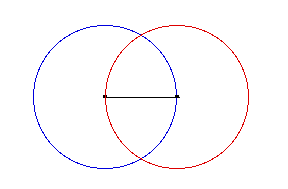
Create two circles using the endpoints as foci. The
entire circle is not necessary, as will be made evident
next. To bisect the line, both circles
must have the same radius. If you only wish to
create a right angle, and not find a midpoint, then the
circles can be of different sizes.
|
|
|
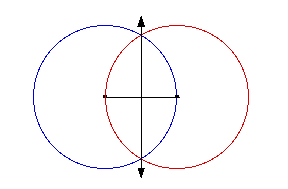
Use a straight edge to draw a second line through the two
points where the circles intersect. This line will cross the
original at a perfect right (90 degree) angle. If the
circles have the same radius, the second straight line will
also pass through the exact mid point on the line
segment.
|
|
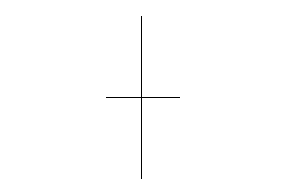
|
This method can be used to create right angles through
specific points as well. just place a point on a line
through which you wish a right angle intersection. Measure
an equal distance to either side of that point and use the
measured points as endpoints.
|
Make a Square (example)
|

|
First make a 90 degree angle with pencil lines.
|
|
|
Placing the focus of the compass at the intersection,
mark equal distances on both lines.
|
|
|
Complete the square at those points making right angles
with a compass.
|
|

|
Remove any extra lines with an eraser. Each side has an
equal measure.
|
Bisect an Angle
Line segments are not the only thing that a compass can spilt into
equal halves. Angles can be bisected as well.
|
Begin with an angle. It can be arbitrary, or carefully
measured.
|
|
|
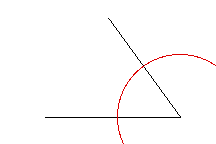
Use a compass to measure off equal distances along the
"legs" of the angle. This is most easily done by drawing the
arc of a circle with its focus at the angle
intersection.
|
|
|
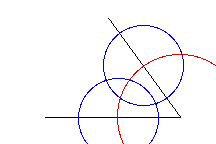
Next, draw two circles of equal radius centering their
foci at the two points where the first circle intersected
the legs of the angle.
|
|
|
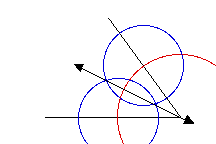
Draw a line through the points where these two circles
intersect. This line splits the angle exactly in two.
|
|
|
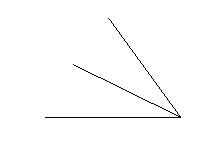
Since any angle can be split in two this way, a compass
can be used to create 90 degree angles from 180 degree
straight lines, and 45 degree angles from 90 degree
intersections.
|
|
Find the Center of a
Circle
It is not always a circle of which one needs to locate the focus.
More often it is an arc, a curve, or partial circle. Still, the same
basic rules apply.
|

|
Start by describing a circle. If only a section of it
appears in a picture, it helps to imagine the whole thing
present.
|
|
|
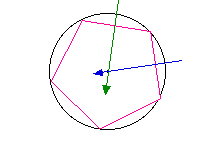
A polygon is inscribed in a circle when each endpoint
lies exactly on the edge of the circle. Any line which
bisects one of the sides of such a polygon at a right angle
will pass through the exact center of the circle.
|
|
|
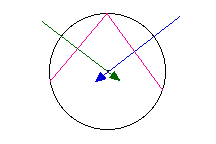
Knowing this, we only need two sides of a polygon to
locate the center. Indeed, we only need two line segments
with endpoints on the circle.
|
|Templates|Triangles|Curves|Rulers|Protractors|Lettering
Guides|Compasses|
[Return
to top of page]