Return to Basic Equipment Menu

Protractors In practice, fields of vision are described in circles and cones which are broken down into 360 degrees. Most artistic endeavors contain an inherent fudge factor, allowing the artist to place lines where they look right merely by "guessing" where they look best. The human brain is very forgiving when angles and depth cues are involved. Sometimes more precision is warranted, and angles must be calculated precisely. A protractor is used to both measure and create proper angles. If you have ever had the occasion to use polar coordinates, then you are already familiar with this sort of device.

Some protractors measure a full 360 degrees, but most stop at 180 degrees and have one straight flat side. Since a full circle is equal to 360 degrees, the exercising of a little basic algebra makes a full circle protractor unnecessary. Since they allow for the measurement and creation of angles in tighter and smaller circumstances, swing arm protractors are also very handy.

Angles are measured from the "station point" which should be made evident in the design of the protractor. Sometimes this is a hole in the device which is meant to center over the intersection of an angle, sometimes it is just an obvious marking along the edge. Measurements taken from other than the station point will be incorrect.

Angle Measurements of Regular Polygons

A regular polygon is any shape consisting of straight sides and angles where each side has an equal length and each angle has an equal degree. Thus a square is a regular polygon because each corner is a 90 degree angle, and each side measures the same length. A rectangle is not because all of its sides need not measure the same.

Sometimes it is necessary to measure out specific shapes when drawing, especially when a specific object is to be rendered in linear perspective. To calculate the angle measures of a regular polygon first count the number of corners (vertices). Next subtract two and then multiply the result by 180 degrees. Finally divide the product by the original number of corners.

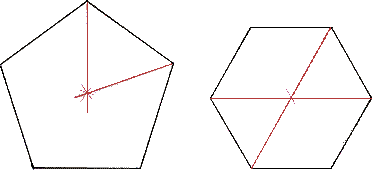
Thus a regular pentagon (five sides) has an angle measure of 108 degrees for each internal angle. [(5-2)*180/5]

To find the center of a regular polygon with an odd number of sides divide the measurement of one corner in half and draw a line from that corner to the other side. Do the same with another corner. The lines will cross at the center of the shape. The same method will work for a polygon with an equal number of sides, but it is simpler just to connect opposite corners.

Regular polyhedrons are 3 dimensional shapes constructed of the regular polygons. There are five regular polyhedrons which are known as the platonic solids.

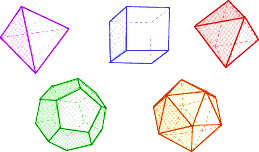
Plato theorized that everything in nature was made from smaller particles, sort of like atoms. He reasoned that these smaller particles must be regular polyhedrons like those pictured above. His concept was based on the classical elements, so his theory may seem strange to our periodic table mentality.